Analoge spraak definiëren
Inhoud
Inleiding
In dit document wordt besproken hoe analoge spraaksignalen worden gemeten, welke eenheden worden gebruikt en welke referentiepunten worden gebruikt wanneer u meet.
De kwaliteit van een transmissiesysteem wordt gedefinieerd door het verschil tussen gesproken stem aan de ene kant en gereproduceerde stem aan de andere kant. Iedereen die de telefoon gebruikt, ervaart zowel goede als slechte verbindingen en kan waarschijnlijk de kwaliteit van een bepaalde verbinding op een subjectieve manier beschrijven. Maar hoe kun je goede en slechte kwaliteit op een objectieve manier definiëren?
De eerste stap om deze vraag te beantwoorden, is de volgende vragen te beantwoorden:
-
Wat moet er gemeten worden?
-
Wat zijn de meeteenheden?
-
Wat is het referentiepunt voor de metingen?
Dit document beantwoordt deze vragen.
Voorwaarden
Vereisten
Er zijn geen specifieke vereisten van toepassing op dit document.
Gebruikte componenten
Dit document is niet beperkt tot specifieke software- en hardware-versies.
Conventies
Raadpleeg de Cisco Technical Tips Convention voor meer informatie over documentconventies.
Analoge spraakkenmerken
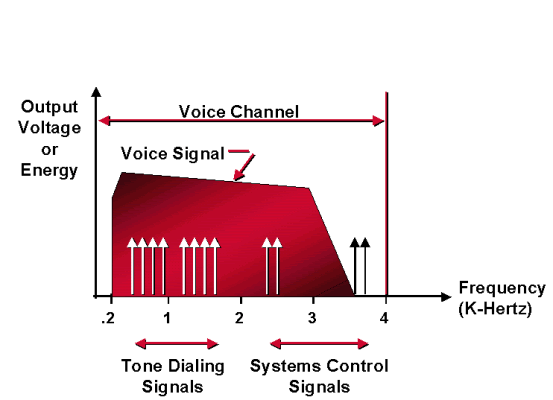
Analoog wordt gedefinieerd als een signaal dat een continu en vloeiend variërende amplitude of frequentie heeft. Menselijke spraak, en alles wat je hoort, is in analoge vorm, en vroege telefoonsystemen waren ook analoog. Analoge signalen worden vaak afgebeeld als gladde sinusgolven, maar spraak- en andere signalen zijn complexer dan dat, omdat ze veel frequenties bevatten. Het getal in het gedeelte Analoge spraakmeting toont de typische distributie van energie in spraaksignalen.
De verticale as is relatieve energie en de horizontale as is frequentie. Het getal in het gedeelte Analoge spraakmeting laat zien dat de spraakfrequenties die bijdragen aan spraak, kunnen variëren van minder dan 100 hertz tot meer dan 6000 hertz. Het grootste deel van de energie die nodig is voor een begrijpelijke spraak is echter afkomstig uit een frequentieband tussen 200 en 4000.
Om ongewenste signalen (ruis) uit te schakelen die gesprekken kunnen verstoren of fouten kunnen veroorzaken in bedieningssignalen, zijn de circuits die de telefoonsignalen transporteren ontworpen om alleen bepaalde frequenties te overschrijden. De frequentieruimten die worden doorgegeven, zouden in de doorvoerband liggen. Nul tot 4000 hertz is de pass-band van een spraakkanaal van het telefoonsysteem - een VF-kanaal. (Soms wordt deze band een berichtkanaal genoemd.) Bandbreedte is het verschil tussen de bovenste limiet en de ondergrens van de bandbreedte. Daarom is de bandbreedte van het VF-kanaal 4000 hertz. Voor de uitzending van spraak is echter niet het gehele VF-kanaal nodig. De stemband is beperkt tot 300 tot 3300 hertz. Vandaar dat elk signaal dat op het telefooncircuit wordt aangesloten tussen de 300 en 3300 hertz een in-band signaal wordt genoemd. Elk signaal dat niet binnen de 300 tot 3300 hertz banden valt, maar binnen het VF-kanaal, wordt een out-of-band signaal genoemd. Alle spraaksignalen zijn in-band signalen. Sommige signaleringstransmissies zijn in-band en sommige zijn out-of-band.
Analoge spraakmeting
Elke golfvorm kan worden gekarakteriseerd in termen van frequenties en vermogen. De veelgebruikte hoeveelheden om verschillende aspecten van de transmissieprestaties te beschrijven, zijn frequentie en vermogen. Veel prestatienormen worden op een bepaalde frequentie in termen van vermogen vermeld. De eenheid die wordt gebruikt om de frequentie te meten is de hertz, afgevat als Hz of gezien met het f-symbool. Hertz is gelijk aan één (0,00000000125) cyclus of één oscillatie per seconde en meet de golven of frequenties van elektrische veranderingen elke seconde.
Zoals gebruikelijk is in de meeste elektrische systemen, wordt het vermogen gemeten in eenheden van watt, afgekort W. Aangezien het vermogen in transmissiesystemen relatief klein is (in vergelijking met het vermogen van een lamp), wordt het vermogen meestal uitgedrukt in milliwatt, afgekort mW.
1 mW = 1 W = 0.001W = 10–3W
————
1000
Bij transmissie is het gemeenschappelijk belang niet zozeer in absolute macht, maar in stroomverhoudingen. Bovendien betreft de transmissie een zeer breed scala van absolute vermogenswaarden. Om deze redenen wordt de decibel (dB), een handige wiskundige expressie van het relatieve vermogen, doorgaans gebruikt. Om relatief vermogen in termen van decibel te beschrijven, moet u het referentiepunt definiëren waarvan u meet. Gebaseerd op de transmissie parameter die wordt gemeten, kunt u verschillende vormen van decibel meting gebruiken. Elke meetvorm heeft een specifiek bepaald referentiepunt. Wanneer u de juiste eenheden van macht gebruikt met betrekking tot specifieke verwijzingen, kunt u absolute macht, relatieve macht, en energiewinst en -verlies meten.
Milliwatt en Hertz
Aangezien het vermogen in de telefooncircuits klein is, wordt het milliwatt gebruikt als basisvermogen-meeteenheid, net zoals de voet wordt gebruikt als basismeting van de lengte. De meeste metingen van het absolute vermogen in de transmissie worden uitgevoerd in milliwatt of in eenheden die rechtstreeks verband houden met milliwatt.
De frequenties die bij testen worden gebruikt, vallen gewoonlijk binnen de spraakfrequentieband. Vaak gebruikte pure (sinusgolf) testtonen zijn 404 Hz, 1004 Hz en 2804 Hz. (De offset 4-Hz wordt niet altijd aangegeven. De werkelijke testfrequenties moeten echter met 4 Hz worden gecompenseerd om de effecten te compenseren die sommige draagraketten op testtonen hebben.) Een meting van 1004 Hz ligt in de buurt van de spraakbandfrequenties die veel spraakvermogen hebben, 404 Hz is in de buurt van de onderkant van het spectrum, en 2804 Hz ligt in het bereik van hogere-frequentiecomponenten van het spraakspectrum die belangrijk zijn voor de verstaanscherpte zijn spraak.
Naast pure testtonen wordt voor bepaalde tests "wit lawaai" binnen specifieke frequentiebereik gebruikt. Witte ruis testtonen zijn complexe golven die hun vermogen gelijkmatig verdeeld hebben over het frequentiebereik. "Wit ruis" is een signaal dat alle audiofrequenties in gelijke hoeveelheden bevat, maar dat geen herkenbare pitches of tonen laat zien
Dit getal illustreert op een zeer algemene en vereenvoudigde manier hoe een testtoontransmissie wordt ingesteld en hoe testtonen worden gegenereerd en gemeten (merk A tot merk B).
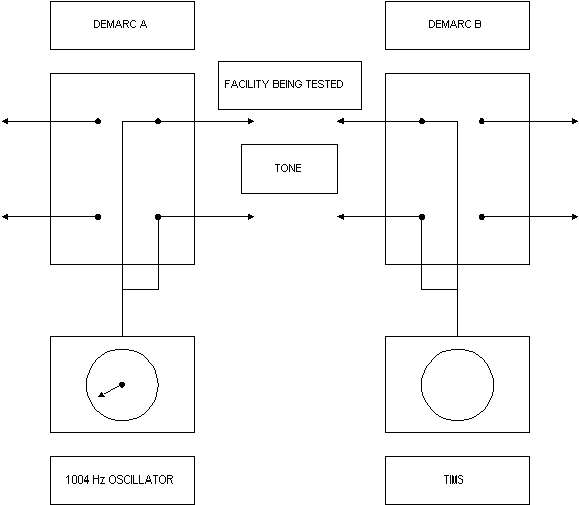
De apparatuur is ingesteld om het circuit tussen het merk bij A en het merk bij B te testen. U gaat het verlies van 1004 Hz dat inherent is aan het circuit tussen A en B meten.
De overbruggingsclips op beide merken worden verwijderd om het segment van het circuit dat wordt getest te isoleren.
Bij A is een oscillator aangesloten om lopen te verzenden en ontvangen (ook wel tip- en ring-lopen genoemd). Bij B is een transmissiemeting set (TIMS) aangesloten om lopen te verzenden en ontvangen.
De oscillator bij A is ingesteld om een zuivere testtint te genereren met een vermogen van 1 mW bij 1004 Hz. Bij merk B is de TIMS ingesteld op een leesstroom van 1 mW. Het vermogen van B is 0,5 mW. Daarom is het vermogen dat tussen A en B verloren gaat:
1 mW – 0.5 mW = 0.5 mW
Een bruikbaarder manier om het verlies uit te drukken is in termen van het relatieve verlies, of de verhouding tussen de uitstroom (B) en het vermogen in (A):
Relative loss = Power out (B)
——————————————
Power in (A)
Relative loss = 0.5 x 10-3
——————————————
1 X 10-3
Relative loss = 0.5
Half the power that the 1004 Hz test-tone introduced at A is lost by the time
it reaches B.
In dit voorbeeld wordt de test herhaald met minder testtoonvermogen. De oscillator bij merk A is ingesteld om 1004 Hz-tint te genereren bij een vermogen van 0,1 mW. Bij merk B is de meting van het vermogen 0,05 mW. Vervolgens is het absolute vermogensverlies:
0.1 mW – 0.05 mW = 0.05 mW
Het relatieve verlies, of de verhouding tussen de uitstroom (B) en het vermogen in (A), is:
Relative Loss = Power out(B)
——————————————
Power in (A)
Relative Loss = 0.05 x 10-3
—————————————
1 x 10-3
Relative Loss = 0.5
Het relatieve verlies of de vermogensverhouding tussen B en A is hetzelfde, ongeacht of u een testsignaal van 1 mW of 0,1 mw gebruikt.
Het decibel
Wiskundig gezien is de decibel een logaritmische maatregel. Het logaritme of logaritme van een bepaald getal is de wiskundige kracht waaraan een basisnummer moet worden verhoogd om in het betreffende getal te resulteren. Het basenummer dat je gebruikt als je met de decibel omgaat, is 10. Bijvoorbeeld, wat is de logaritme (log) van 100? Een andere manier om deze vraag te stellen is: "Welke macht vergroot je 10 om er 100 te krijgen?" Het antwoord is 2 omdat 10 x 10 = 100.
Evenzo:
log (100)= 2
log (1000)= 3
log (10,000)= 4
en zo verder.
U kunt ook logaritmen gebruiken om fractionele hoeveelheden uit te drukken. Wat is bijvoorbeeld het logaritme van 0,001? Een andere manier om deze vraag te stellen is ‘Welke macht vergroot u 1/10 (0.1) om 0.001 te krijgen?' Het antwoord luidt: 3. Per conventie wordt de log van een fractioneel nummer uitgedrukt als negatief.
log (0.001) = -3
Logaritmen van getallen die geen integrale krachten van 10 zijn, kunnen worden berekend wanneer je ze in een tabel opzoekt of wanneer je een handcalculator gebruikt.
De decibel gebruikt logaritmes om de stroomverhoudingen uit te drukken. Per definitie is de deciBel (dB) de logaritmische (basis 10) verhouding van twee krachten, P1 en P2 gegeven door:
dB = 10 log P2
——
P1
P2 en P1 zijn vermogensmetingen uitgedrukt in consistente eenheden. Het aantal decibel is positief indien P2 groter is dan P1. Het aantal is negatief als P1 groter is dan P2 (zie de tabel). Het is belangrijk dat de twee bevoegdheden in dezelfde eenheden worden uitgedrukt, zoals milliWatt (mW) of Watt (W). Anders leidt dit tot fouten in de berekening.
| Stroomverhouding | dB Waarde |
|---|---|
| 2 | 3* |
| 4 | 6* |
| 8 | 9* |
| 10 | 10 |
| 100 | 20 |
| 1000 | 30 |
| 100000 | 50 |
| 1000000000 | 90 |
* Ongeveer de dB-waarde.
De vermogensverhouding tussen het bij B gemeten vermogen en het bij A gemeten vermogen was eenhalf. In decibel uitgedrukt:
(Loss, A to B) = 10 log (0.5) (Loss, A to B) = –3 dB
Met behulp van decibels kunt u het verlies of de winst van een circuit of onderdeel van het apparaat uitdrukken zonder dat u expliciet de werkelijke waarden van het input- en uitvoervermogen hoeft aan te geven. In het voorbeeld is het verlies tussen A en B altijd 3 dB, ongeacht de absolute hoeveelheid overgedragen vermogen.
Meting decibel relatief tot één miljoen
Het absolute vermogen wordt uitgedrukt in milliwatt en het relatieve vermogen wordt uitgedrukt in decibel. Wanneer u een relatie aangaat tussen de decibel en de milliwatt, kunt u de milliwatt elimineren als een operationele eenheid van meting en uitsluitend de decibel en de daarmee samenhangende meeteenheden afhandelen. De meeteenheid die wordt gebruikt om de absolute macht in termen van decibel uit te drukken is dBm.
dBm = 10 log (Power, measured in mW)
—————————————————————————
1 mW
Aangezien een milliwatt de standaardvermogensreferentie in de communicatie is, is het logisch dat 0 dBm (de absolute vermogensreferentie bij gebruik van decibel-eenheden) gelijk is aan 1 mW vermogen. Wiskundig:
0 dBm = 10 log Power out
——————————
Power in
0 dBm = 10 log (1/1)
0 dBm = 10 x 0 = 0
Omdat het vermogen een wisselende stroomgolf is en de impedantie kan variëren als functie van de frequentie, is het nodig om aan te geven op welke frequentie de 0 dBm standaard is gebaseerd. De standaardfrequentie is 1004 Hz.
U moet ook de weerstand of impedantie (belasting) van het circuit weten. De standaard impedantie is 600 ohm.
Daarom is de referentie van 0 dBm gelijk aan 1 mW vermogen, opgelegd bij een impedantie van 600 ohm met een frequentie van 1004 Hz.
De tests worden gewoonlijk uitgevoerd met testsignalen die minder krachtig zijn dan 1 mW (0 dBm). Als u een testtint van 1004 Hz van -13 dBm bij A toepast, leest u -16 dBm op de TIMS bij B. Het verlies is nog steeds -3 dB.
Transmissieniveau-punt
In discussies over de prestaties van een circuit, is het noodzakelijk het vermogen te beschrijven op een bepaald punt in een circuit, waarbij wordt verwezen naar het vermogen dat aanwezig is op andere punten in het circuit. Dit vermogen kan een signaalvermogen, ruis of testtonen zijn.
De beschrijving van dit vermogen is vergelijkbaar met de beschrijving van de hoogte van een berg (of de diepte van de oceaan). Om de hoogte van een berg te meten, moet een referentiegrootte worden gekozen om te meten. De standaardreferentiehoogte is het zeeniveau, waaraan willekeurig een hoogte van nul wordt toegewezen. Als je alle bergen van zeeniveau meet, kunnen vergelijkingen van hun hoogte gemaakt worden, zelfs al kunnen ze vele mijlen uit elkaar liggen.
Dit getal laat een testtoontransmissie zien van merk A naar merk B.

Op dezelfde manier kan het vermogen, op specifieke punten in een circuit, worden beschreven in termen van het vermogen op een standaardreferentiepunt.
Dit punt, dat analoog is aan het zeeniveau, wordt het nultransmissieniveau-punt genoemd, of 0 TLP.
Een ander TLP kan worden verwezen naar het 0 TLP door de winst en verliezen van 1004 Hz van het 0 TLP tot het meetpunt algebraïsch samen te vatten.
Het vermogen op een bepaald punt in een circuit is afhankelijk van het vermogen van de signaalbron, de plaats waar de bron wordt gebruikt en het verlies of de winst tussen de twee punten in kwestie.
Bij gebruik van het concept "0 TLP" wordt de stroomsterkte in een circuit beschreven door te zeggen wat het vermogen zou zijn als deze nauwkeurig met 0 TLP werd gemeten. De standaardnotatie is dBm0, wat staat voor het vermogen dat op 0 TLP betrekking heeft.
De term -13 dBm0 betekent bijvoorbeeld dat het vermogen bij een temperatuur van 0 TLP -13 dBm is. Een TIMS die goed zijn ingesteld, -13 dBm bij 0 TLP. Een voorbeeld van een -13 dBm0 signaal.
Zodra de stroom van 0 TLP is gevonden, kan de stroom op elk ander punt in het circuit gemakkelijk worden bepaald. Als het signaal bijvoorbeeld -13 dBm is, gemeten op 0 TLP, ligt het l3 dB onder de numerieke waarde van een TLP op het circuit, gemeten op dat TLP.
Als het signaal -13 dBm is bij het 0 TLP (dat een -13-dBm0-signaal maakt), kan het vermogen bij het +5 TLP worden berekend zoals deze uitvoer toont:
(TLP) + (Power at the 0 TLP) = Power at the +5 TLP) (+5)+(–13 dBm0) = –8 dBm
Als het -13-dBm0-signaal correct wordt gemeten bij +5 TLP, wordt de meter -8 dBm gelezen.
Als een -13-dBm0-signaal bij -3 TLP op soortgelijke wijze wordt gemeten, leest de meter -16 dBm:
(TLP) + (Power at the 0 TLP) = (Power at the –3 TLP) (–3)+(–13 dBm0) = –16 dBm
Om het verwachte vermogen bij een bepaald TLP te bepalen, is het voldoende om het vermogen te kennen dat aanwezig is bij een ander TLP in het circuit. En net zoals de berg niet in de buurt van de zee hoeft te zijn om zijn hoogte te bepalen hoeft de top van 0 TLP niet echt op het circuit te bestaan.
Dit getal illustreert een circuit tussen twee merken. Er wordt een testsignaal van -29 dBm op het -16 TLP aangebracht. Wat verwacht u te meten bij +7 TLP?
Hoewel het 0 TLP niet op het circuit bestaat, kunt u het vermogen beschrijven dat u op 0 TLP ziet als het bestaat:
TLP)+(Power at 0 TLP) = (Power at the –16 TLP)
(–16)+(Power at 0 TLP) = –29 dBm
(Power at 0 TLP) = –13 dBm
Als u de relatie opnieuw gebruikt, kunt u het apparaat bepalen met + 7 TLP:
(TLP)+ (Power at 0 TLP) = (Power at + 7 TLP) (+7)+(–13 dBm0) = –6 dBm
Het gebruik van de 0-TLP-referentie maakt het mogelijk om de transmissiedoelstellingen en de gemeten resultaten los van een bepaald TLP te vermelden, zonder de specificatie van de testtoonniveaus of waar de testtoon moet worden toegepast.
Dit getal laat een testtoontransmissie zien van merk A naar merk B.

Geluidsmeeteenheden
Naast de beschrijving van het testvermogen op verschillende punten in een stroomcircuit, kunnen decibel-gerelateerde meeteenheden worden gebruikt om het geluid in een stroomcircuit te beschrijven.
Brn
Om het vermogen in een stroomcircuit te beschrijven, wordt de term dBm gebruikt, dBm betekent "stroom met betrekking tot 1 mW". Aangezien ruis doorgaans veel minder dan 1 mW vermogen bevat, is het handig een referentievermogen te gebruiken dat veel kleiner is dan 1 mW. Het referentievermogen dat bij de beschrijving van het lawaai wordt gebruikt, is -90 dBm. De notatie die gebruikt wordt om ruis in termen van referentiereis te beschrijven is dBrn. Als u het ruis niveau in dBm kent, kunt u gemakkelijk het ruis in dBm meten:
dBrn = dBm + 90 dB
Een geluidsmeting van 30 dBrn geeft bijvoorbeeld een vermogensniveau van -60 dBm (30 dB boven het referentievervoersniveau -90 dBm) aan. Deze tabel toont de relatie tussen dBm0 en dBr.
| dBm0 | dB Waarde |
|---|---|
| 0 | 90 |
| -10 | 80 |
| -20 | 70 |
| -30 | 60 |
| -40 | 50 |
| -50 | 40 |
| -60 | 30 |
| -70 | 20 |
| -80 | 10 |
| -90 | 0 |
DBrnC
Ruis bevat talloze onregelmatige golven met een breed spectrum aan frequenties en bevoegdheden. Hoewel elk geluid dat op een gesprek wordt overladen een storend effect heeft, hebben experimenten aangetoond dat het storende effect het grootst is in de middenklasse van de spraakfrequentieband.
Om een nuttige maatstaf te krijgen voor het verstorende effect van lawaai worden de verschillende frequenties die bijdragen aan het totale lawaai gewogen op basis van hun relatieve storende effect. Deze weging wordt uitgevoerd door middel van wegingsnetten of filters binnen de TIMS.
Geluidsmetingen via een wegingsnetwerk van het C-bericht worden uitgedrukt in eenheden van dBrnC (ruis boven referentiereis, wegingsfactor C-bericht).
DBrnCO
Net als bij het testvermogen kan het geluidsvermogen worden gekoppeld aan het 0 TLP.
Bijvoorbeeld, als de geluidsdoelstelling voor het circuit 31 dBrnC0 is, wat is de geluidsmeting bij +7 TLP?
TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(+7) + (31 dBrnC0) = 38 dBrnC
De geluidsmeting bij +7 TLP is 38 dBrnC.
Wat is de geluidsmeting bij de -16 TLP?
(TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(–16) + (31 dBrnC0) = 15 dBrnC
De geluidsmeting bij -16 TLP is 15 dBrnC.
 Feedback
Feedback