アナログ音声の定義
内容
概要
このドキュメントでは、アナログ音声信号の測定方法、使用する単位、および測定時に使用する参照点について説明します。
伝送システムの品質は、一端で話される音声と、他端で再現される音声の差によって定義されます。電話を使用したことのある人であれば、接続状態のよいときと悪いときの両方を経験していて、おそらく、接続状態の品質を主観的な方法で説明することができるかと思います。それでは、客観的な方法で品質の良し悪しを定義するには、どうすればよいのでしょうか。
伝送の分野では、次の項目を判断することが、この質問に答える最初のステップとなります。
-
測定の対象は何であるか。
-
測定単位は何であるか。
-
測定の参照点は何であるか。
このドキュメントでは、これらの質問に答えます。
前提条件
要件
このドキュメントに特有の要件はありません。
使用するコンポーネント
このドキュメントの内容は、特定のソフトウェアやハードウェアのバージョンに限定されるものではありません。
表記法
ドキュメント表記の詳細については、『シスコ テクニカル ティップスの表記法』を参照してください。
アナログ音声の特性
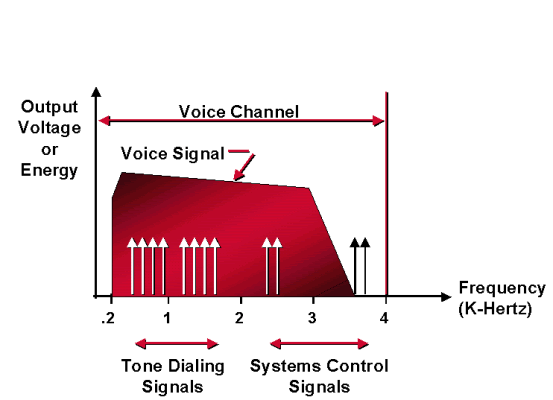
アナログとは、継続的に滑らかに変動する振幅や周波数を伴う信号と定義されます。人間の話声など、耳に聞こえるものはすべてアナログ形式で、初期の電話システムもまたアナログ形式でした。多くの場合、アナログ信号は滑らかな正弦波で表現されますが、音声やその他の信号はもっと複雑で多様な周波数が含まれています。「アナログ音声の測定」セクションの図は、音声信号の典型的なエネルギーの分布を示しています。
縦軸は相対的なエネルギー、横軸は周波数です。「アナログ音声の測定」セクションの図には、会話を構成する音声周波数は、100 ヘルツ未満から 6000 ヘルツ以上にまで及ぶことが示されています。ただし、理解可能な会話に必要とされるエネルギーのほとんどは、200 〜 4000 の周波数の帯域に含まれています。
会話を妨害したり、制御信号のエラーを引き起こす可能性がある不要な信号(ノイズ)を除去するため、電話信号を伝送する回線は、特定の帯域の周波数だけを渡す設計になっています。この渡される周波数の帯域は、パスバンドに収まっていると言われています。0 ~ 4000ヘルツは、電話システムの音声チャネル – VFチャネルのパスバンドです。(この帯域はメッセージチャネルと呼ばれることもあります)。 帯域幅とは、パスバンドの上限と下限の差です。したがって、VF チャネルの帯域幅は 4000 ヘルツです。ただし、会話の伝送に VF チャネル全体が必要となるわけではありません。音声のパスバンドは、300 〜 3300 ヘルツに制限されています。この理由から、電話回線の 300 ~ 3300 ヘルツの帯域で伝送される信号をインバンド信号と呼びます。VF チャネルに含まれている 300 ~ 3300 ヘルツの帯域外の信号をアウトオブバンド信号と呼びます。すべての音声信号は、インバンド信号です。信号の伝送にはインバンドもあれば、アウトオブバンドもあります。
アナログ音声の測定
すべての波形は、周波数と出力で示すことができます。さまざまな面の伝送パフォーマンスを記述するときに、一般的に使用される数量は、周波数と出力です。パフォーマンス標準の多くは、特定の周波数における出力で表記されています。周波数の測定に使用する単位はヘルツで、Hz と略記されますが、f 記号が付記される場合もあります。ヘルツは、1 サイクルまたは 1 振幅/秒に相当し、電気的な波形または周波数の 1 秒ごとの変動を表します。
ほとんどの電気システムで一般的なように、電力の単位はワットで表し、W と略記します。伝送システムで発生する電力は(電球の電力に比べて)比較的小さいため、通常、ミリワットで表現され、mW と略記します。
1 mW = 1 W = 0.001W = 10–3W
————
1000
伝送の分野で、一般的に取り扱われるのは、絶対電力値よりも電力比です。また、伝送に関係する絶対電力値の範囲は非常に広いものになります。これらの理由から、相対電力の便利な表示方式であるデシベル(dB)が一般的に使用されます。デシベルに換算して相対電力を表すには、測定の基準となる参照点を定義する必要があります。測定する伝送パラメータに基づいて、さまざまな形式のデシベル測定値を使用できます。各形式の測定値には、それぞれに定義された参照点があります。それぞれの参照点に相関する適切な電力の単位を使用すると、絶対電力、相対電力、電力ゲイン、および電力損失の値を表現できます。
ミリワットとヘルツ
電話回線内の電力は小さいため、(基本的な長さの測定単位にメートルが使用されるように)基本的な電力の測定単位にはミリワットが使用されます。伝送の分野では、通常、絶対電力の測定値にはミリワットの単位、またはミリワットに直接関連する単位が使用されます。
テストでは、通常、音声周波数の帯域内の周波数が使用されます。一般的に使用される純音(正弦波)のテスト トーンは、404 Hz、1004 Hz、および 2804 Hz です(4 Hz のオフセット値は、必ずしも表記されません。ただし、実際のテスト周波数は4 Hzでオフセットし、一部のキャリア設備がテストトーンに与える影響を補正する必要があります)。1004 Hzの測定は音声出力の多い音声帯域周波数に近く、404 Hzの測定は周波数に低にスピーチの了解度
一部のテストでは、純音のテスト トーンに加えて、特定の周波数帯域の「ホワイト ノイズ」が使用されます。ホワイト ノイズのテスト トーンは、対象の周波数帯域に均等に出力が分散された複雑な波形です。「ホワイト ノイズ」とは、全域の音声周波数が均等に含まれた信号で、ピッチやトーンを知覚できるものではありません。
次の図は、特に一般的かつ簡略化した方法で、(分界点 A と分界点 B の間の)テスト トーンの伝送がどのように準備され、テスト トーンがどのように生成されて測定されるかを示しています。
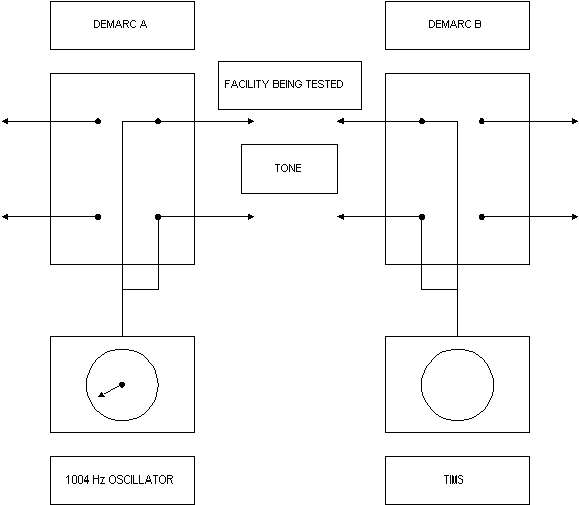
機器は、分界点 A と分界点 B の間の回線のテスト用にセット アップされています。これにより、A と B の間の回線に内在する 1004 Hz での損失が測定されます。
テスト中の回線のセグメントを切り分けるため、それぞれの分界点のブリッジング クリップは外されています。
A では、送信リード線と受信リード線(チップ リード線とリング リード線ともいいます)に発振器が接続されています。 B では、Transmission Measuring Set(TIMS; 伝送測定器)が、送信リード線と受信リード線に接続されています。
A の発振器は、1004 Hz の純音のテスト トーンを 1 mW の出力で生成するように設定されています。分界点 B の TIMS は、1 mW の範囲の電力を読み取るように設定されています。B での電力の読み取り値は、0.5 mW です。したがって、A と B の間の電力損失は、次のようになります。
1 mW – 0.5 mW = 0.5 mW
損失を表すのにさらに便利な方法は相対損失で、次のように出力電力(B)と入力電力(A)の比で表します。
Relative loss = Power out (B)
——————————————
Power in (A)
Relative loss = 0.5 x 10-3
——————————————
1 X 10-3
Relative loss = 0.5
Half the power that the 1004 Hz test-tone introduced at A is lost by the time
it reaches B.
次の例では、さらに低出力のテスト トーンで再度テストを行っています。分界点 A の発振器は、1004 Hz のトーンを 0.1 mW の出力で生成するように設定されています。分界点 B での電力測定値は 0.05 mW です。この場合、絶対損失電力は次のようになります。
0.1 mW – 0.05 mW = 0.05 mW
相対損失、つまり出力電力(B)と入力電力(A)の比は、次のようになります。
Relative Loss = Power out(B)
——————————————
Power in (A)
Relative Loss = 0.05 x 10-3
—————————————
1 x 10-3
Relative Loss = 0.5
相対損失、つまり B と A の電力比は、使用するテスト信号が 1 mW のときも、0.1 mw のときも変わりません。
デシベル
数学的には、デシベルは対数による測定単位です。ある数の対数(log)とは、底となる数値を累乗してその数値が算出される指数を表します。デシベルを処理するときに使用する基数は10です。たとえば、100の対数(ログ)は何ですか。別の言い方で質問するなら、「10 を何乗すると 100 になるでしょうか」。 10 x 10 = 100 であるため、答えは 2 です。
同様に、
log (100)= 2
log (1000)= 3
log (10,000)= 4
等。
また、対数を使用して、小数(分数)の値を表すこともできます。たとえば、0.001 の対数はいくつでしょうか。別の言い方で質問するなら、「1/10(0.1)を何乗すると、0.001 になるでしょうか」。 答えは3です。表記法では、分数のログは負として表されます。
log (0.001) = -3
10 の累乗でない数の対数を計算する場合は、対数表で調べるか、電卓を使用します。
デシベルでは、対数を使用して電力比を表します。定義では、デシベル(dB)は、10 を底とする 2 つの電力 P1 と P2 の対数比で、次のように示されます。
dB = 10 log P2
——
P1
P2 と P1 は、共通の単位で表される電力値です。デシベルの数は、P2がP1より大きい場合は正です。P1がP2より大きい場合は負です(表を参照してください)。 重要な点は、2 つの電力を同じ単位(ミリワット(mW)、ワット(W)など)で表すことです。 そうしなかった場合、正しい計算結果は算出されません。
| 電力比 | dB 値 |
|---|---|
| 0 | 3* |
| 4 | 6* |
| 8 | 9* |
| 10 | 10 |
| 100 | 20 |
| 1,000 | 30 |
| 100000 | 50 |
| 1000000000 | 90 |
* 近似 dB 値
B で測定された電力と A で測定された電力の電力比は、1/2 でした。これをデシベルで表すと、次のようになります。
(Loss, A to B) = 10 log (0.5) (Loss, A to B) = –3 dB
デシベルを使用すると、入力電力と出力電力の実際の値を明示的に表記しなくても、回線や機器の部分での損失やゲインを表すことができます。たとえば、A と B の間の損失は、伝送される電力の絶対量にかかわらず、常に 3 dB です。
1 ミリワットに相当するデシベルの測定単位
絶対電力はミリワットで表し、相対電力はデシベルで表します。デシベルとミリワットの間に関係を確立すると、測定上の作業単位としてミリワットは扱わずに、デシベルとそれに関連する測定単位だけを取り扱うことが可能になります。絶対電力をデシベルで表すときに使用する測定単位は、dBm です。
dBm = 10 log (Power, measured in mW)
—————————————————————————
1 mW
通信の分野では、ミリワットが標準の電力基準であることから、必然的に、0 dBm(デシベルの単位を使用する場合の絶対電力の基準)は、1 mW の電力に相当します。数学的には、次のように示すことができます。
0 dBm = 10 log Power out
——————————
Power in
0 dBm = 10 log (1/1)
0 dBm = 10 x 0 = 0
電力は交流電流波形であり、インピーダンスは周波数の関数として変動することがあるため、基準の 0 dBm が基準とする周波数を表記する必要があります。ここでは、基準周波数を 1004 Hz とします。
また、回線の抵抗またはインピーダンス(負荷)を把握しておく必要があります。ここでは、基準インピーダンスを 600 Ω とします。
したがって、0 dBm の表記は、周波数 1004 Hz、インピーダンス 600 Ω での 1 mW の電力に相当します。
通常、テストは、1 mW(0 dBm)未満の電力のテスト信号を使用して実行されます。 Aで–13 dBmの1004 Hzテストトーンを適用した場合、BのTIMSでは–16 dBmと表示されます。損失は–3 dBのままです。
伝送基準点(TLP)
回線のパフォーマンスを取り上げる場合、回線内の特定地点の電力を、回線内の他の地点で発生する電力に対する基準として表記する必要があります。このときの電力には、信号電力、ノイズ、テスト トーンなどが当てはまります。
この電力の表記は、山の高さ(または海の深さ)の表記に類似しています。 山の高さを測定するには、測定の元となる基準の高さを選択する必要があります。一般的な基準の高さは海面で、無条件で高さ 0 が割り当てられます。すべての山を海面から測定すると、それぞれの山が何キロ離れていても、山の高さを比較できるようになります。
次の図は、分界点 A から分界点 B へのテスト トーンの伝送を示しています。

同じように、電力の場合も、回線内の各地点の電力を、標準の参照点の電力を基に表すことができます。
海面に相当するこの地点は、0 の伝送基準点、つまり 0 TLP と呼びます。
その他の TLP は、0 TLP から測定地点までの 1004 Hz でのゲインと損失の代数和を取ることにより、0 TLP の基準を参照できます。
回線内の特定の地点で計測される電力は、信号の送信元での出力、信号の送信元がある場所、および対象の 2 つの地点間の損失またはゲインによって決まります。
0 TLP の概念を使用する場合、回線内の電力は、0 TLP で厳密に測定したものとして計測される電力で表記されます。標準の表記法は dBm0 で、これは 0 TLP の基準を参照している電力を意味します。
たとえば、-13 dBm0という用語は、0 TLPでの電力が–13 dBmであることを意味します。正しくセットアップされた TIMS によって、0 TLP で -13 dBm が測定されています。ここでは、-13 dBm0 の信号を例として使用します。
0 TLP の電力が判明すると、回線内のその他の地点の電力は簡単に算出できます。たとえば、0 TLP で測定された信号が -13 dBm の場合、回線上のその他の TLP で測定される数値は、13 dB 低い数値になります。
信号が 0 TLP で -13 dBm の場合(-13-dBm0 の信号の場合)、+5 TLP での電力は、次の出力に示すように算出できます。
(TLP) + (Power at the 0 TLP) = Power at the +5 TLP) (+5)+(–13 dBm0) = –8 dBm
-13-dBm0 の信号を +5 TLP で正確に測定すると、計器で -8 dBm が読み取られます。
同様に、-13-dBm0 の信号を -3 TLP で測定すると、計器で -16 dBm が読み取られます。これは、次のように算出できます。
(TLP) + (Power at the 0 TLP) = (Power at the –3 TLP) (–3)+(–13 dBm0) = –16 dBm
特定の TLP で予測される電力を算出するには、回線内のいくつかの TLP で計測される電力を知っておくだけで十分です。また、山の高さを測定するときに山が海の近くになくてもかまわないように、0 TLP は、実際に回線上に存在していなくてもかまいません。
次の図は、2 つの分界点の間の回線を示しています。-16 TLP で、-29-dBm のテスト トーン信号が印加されています。+7 TLP で測定される値には、いくつが予測されるでしょうか。
回線上に 0 TLP が存在していない場合であっても、仮に存在していた場合に 0 TLP で確認される電力は、次のように表すことができます。
TLP)+(Power at 0 TLP) = (Power at the –16 TLP)
(–16)+(Power at 0 TLP) = –29 dBm
(Power at 0 TLP) = –13 dBm
さらに、この関係を使用して、+ 7 TLP での電力を次のように算出できます。
(TLP)+ (Power at 0 TLP) = (Power at + 7 TLP) (+7)+(–13 dBm0) = –6 dBm
0 TLP の基準を使用すると、伝送目標と測定結果を、特定の TLP に依存することなく表記でき、テスト トーンのレベルや印加された地点を明記する必要もありません。
次の図は、分界点 A から分界点 B へのテスト トーンの伝送を示しています。

ノイズの測定単位
デシベル関連の測定単位は、回線内の各地点でのテストトーンの電力表記のほか、回線内に発生するノイズを表す場合にも使用できます。
dBrn
回線内の電力を表すために dBm の表記を使用します。これは、「1 mW を基準とした電力」を意味します。 通常、ノイズの電力は 1 mW よりはるかに低いため、1 mW よりもかなり小さい基準電力を使用すると便利です。ここでは、ノイズの表記に使用する基準電力を -90 dBm とします。ノイズを基準ノイズの単位で表記するときに使用する表記法は、dBrn です。ノイズ レベルの dBm が判れば、ノイズの dBrn は、次のように簡単に算出できます。
dBrn = dBm + 90 dB
たとえば、ノイズの測定単位 30 dBrn は、電力レベルで -60 dBm であることを示しています(-90 dBm の基準ノイズ レベルよりも 30 dB 大きい値)。 次の表に、dBm0 と dBrn の関係を示します。
| dBm0 | dB 値 |
|---|---|
| 0 | 90 |
| -10 | 80 |
| -20 | 70 |
| -30 | 60 |
| -40 | 50 |
| -50 | 40 |
| -60 | 30 |
| -70 | 20 |
| -80 | 10 |
| -90 | 0 |
DBrnC
ノイズには、さまざまな周波数と電力の不規則な波形が数多く含まれています。会話に重畳されるノイズには干渉効果がありますが、実験により、干渉効果は中域の音声周波数帯域で最大になることが示されています。
ノイズの干渉効果の有用な測定値を取得するには、ノイズ全体を構成する各周波数を、それぞれの相対的な干渉効果に基づいて重み付けします。この重み付けは、TIMS 内部の聴感補正回路(つまりフィルタ)を経由して、実行されます。
C メッセージ聴感補正回路を経由したノイズの測定値は、dBrnC の単位(基準ノイズの C メッセージ聴感補正回路を超えるノイズ)で表されます。
DBrnCO
テスト トーンの電力と同じように、ノイズの電力は、0 TLP を基準とすることができます。
たとえば、回線でのノイズ目標値が 31 dBrnC0 の場合、+7 TLP でのノイズの測定値はいくつになるでしょうか。
TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(+7) + (31 dBrnC0) = 38 dBrnC
+7 TLP でのノイズ測定値は、38 dBrnC です。
–16 TLP でのノイズ測定値はいくつになるでしょうか。
(TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(–16) + (31 dBrnC0) = 15 dBrnC
-16 TLP でのノイズ測定値は、15 dBrnC です。
 フィードバック
フィードバック