Définition de la voix analogique
Contenu
Introduction
Ce document explique comment les signaux vocaux analogiques sont mesurés, les unités utilisées et les points de référence utilisés lors de la mesure.
La qualité d'un système de transmission est définie par la différence entre la voix vocale à une extrémité et la voix reproduite à l'autre extrémité. Toute personne qui utilise le téléphone connaît des connexions bonnes et mauvaises, et peut probablement décrire la qualité d'une connexion particulière d'une manière subjective. Mais comment définir objectivement la bonne et la mauvaise qualité ?
Dans la transmission, la première étape pour répondre à cette question est de se prononcer sur ces questions :
-
Que faut-il mesurer ?
-
Quelles sont les unités de mesure ?
-
Quel est le point de référence pour les mesures ?
Ce document répond à ces questions.
Conditions préalables
Conditions requises
Aucune spécification déterminée n'est requise pour ce document.
Components Used
Ce document n'est pas limité à des versions de matériel et de logiciel spécifiques.
Conventions
Pour plus d'informations sur les conventions utilisées dans ce document, reportez-vous à Conventions relatives aux conseils techniques Cisco.
Caractéristiques vocales analogiques
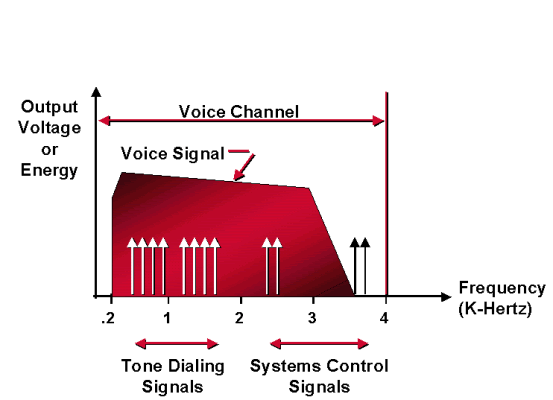
L'analogique est défini comme un signal dont l'amplitude ou la fréquence varient en continu et en douceur. La parole humaine, et tout ce que vous entendez, est sous forme analogique, et les premiers systèmes téléphoniques étaient également analogiques. Les signaux analogiques sont souvent représentés comme des ondes sinusoïdales lisses, mais les signaux vocaux et autres sont plus complexes que cela, puisqu'ils contiennent de nombreuses fréquences. La figure de la section Mesure de la voix analogique montre la distribution typique d'énergie dans les signaux vocaux.
L'axe vertical est l'énergie relative et l'axe horizontal est la fréquence. La figure de la section Mesure de la voix analogique montre que les fréquences vocales qui contribuent à la parole peuvent passer de moins de 100 hertz à plus de 6 000. Cependant, la plus grande partie de l'énergie nécessaire à une parole intelligible se trouve dans une bande de fréquences comprise entre 200 et 4000.
Afin d'éliminer les signaux indésirables (bruit) qui peuvent perturber les conversations ou provoquer des erreurs dans les signaux de contrôle, les circuits qui transportent les signaux téléphoniques sont conçus pour ne transmettre que certaines fréquences. Les plages de fréquences qui sont passées sont dites dans la bande de passe. Zéro à 4 000 hertz est la bande de passe d'un canal vocal du système téléphonique - un canal VF. (Parfois, cette bande est appelée canal de message.) La bande passante est la différence entre la limite supérieure et la limite inférieure de la bande passante. Par conséquent, la bande passante du canal VF est de 4000 hertz. Cependant, la transmission de la parole ne nécessite pas la totalité du canal VF. La bande de passe vocale est limitée à 300 à 3 300 hertz. Par conséquent, tout signal transporté sur le circuit téléphonique qui se situe entre 300 et 3300 hertz est appelé un signal intrabande. Tout signal qui ne se trouve pas dans les bandes 300 à 3 300 hertz, mais qui se trouve dans le canal VF, est appelé signal hors bande. Tous les signaux vocaux sont des signaux intrabande. Certaines transmissions de signalisation sont en bande et d’autres hors bande.
Mesure de la voix analogique
Toute forme d'onde peut être caractérisée en termes de fréquences et de puissance. Les quantités couramment utilisées pour décrire divers aspects des performances de transmission sont la fréquence et la puissance. De nombreuses normes de performance sont énoncées en termes de puissance à une fréquence particulière. L'unité utilisée pour mesurer la fréquence est le hertz, abrégé en Hz ou vu avec le symbole f. Hertz équivaut à un cycle (0,0000000125) ou à une oscillation par seconde et mesure les ondes ou les fréquences des changements électriques chaque seconde.
Comme dans la plupart des systèmes électriques, la puissance est mesurée en unités de watts, abrégée W. Comme la puissance rencontrée dans les systèmes de transmission est relativement faible (par rapport à la puissance d'une ampoule), la puissance est généralement exprimée en milliwatts, en mW abrégé.
1 mW = 1 W = 0.001W = 10–3W
————
1000
Dans la transmission, l'intérêt commun réside dans les rapports de puissance plutôt que dans le pouvoir absolu. En outre, la transmission concerne un éventail extrêmement large de valeurs de puissance absolue. Pour ces raisons, une expression mathématique pratique de la puissance relative, le décibel (dB), est couramment utilisée. Afin de décrire la puissance relative en termes de décibels, vous devez définir le point de référence à partir duquel vous mesurez. En fonction du paramètre de transmission mesuré, vous pouvez utiliser différentes formes de mesure du décibel. Chaque forme de mesure comporte un point de référence spécifique. Lorsque vous utilisez les unités de puissance appropriées liées à des références spécifiques, vous pouvez mesurer la puissance absolue, la puissance relative et les gains et pertes de puissance.
Milliwatt et Hertz
Comme la puissance des circuits téléphoniques est faible, le milliwatt est utilisé comme unité de mesure de la puissance de base, tout comme le pied est utilisé comme mesure de base de la longueur. La plupart des mesures de la puissance absolue dans la transmission sont faites en milliwatts ou en unités directement liées aux milliwatts.
Les fréquences utilisées dans les tests se situent généralement dans la bande de fréquences vocales. Les tonalités de test pures (onde sinusoïdale) couramment utilisées sont 404 Hz, 1004 Hz et 2804 Hz. (Le décalage de 4 Hz n'est pas toujours indiqué. Toutefois, les fréquences d’essai réelles devraient être décalées de 4 Hz afin de compenser les effets que certaines installations de porteuse ont sur les tonalités d’essai.) Une mesure de 1 004 Hz est proche des fréquences de bande vocale qui transportent une grande partie de la puissance vocale, 404 Hz est proche de l’extrémité basse du spectre et 2 804 Hz est dans la plage des composantes de plus haute fréquence du spectre vocal qui sont importantes pour l’intelligibilité du discours.
En plus des tons d'essai purs, le « bruit blanc » dans des plages de fréquences spécifiques est utilisé pour certains essais. Les sons de test de bruit blanc sont des formes d'onde complexes dont la puissance est répartie uniformément sur la gamme de fréquences concernée. « Bruit blanc » est un signal qui contient toutes les fréquences audio en quantités égales, mais qui ne manifeste aucun ton ou ton reconnaissable
Cette figure illustre, de manière très générale et simplifiée, comment une transmission de tonalité d'essai est configurée et comment les tonalités d'essai sont générées et mesurées (demarc A à demarc B).
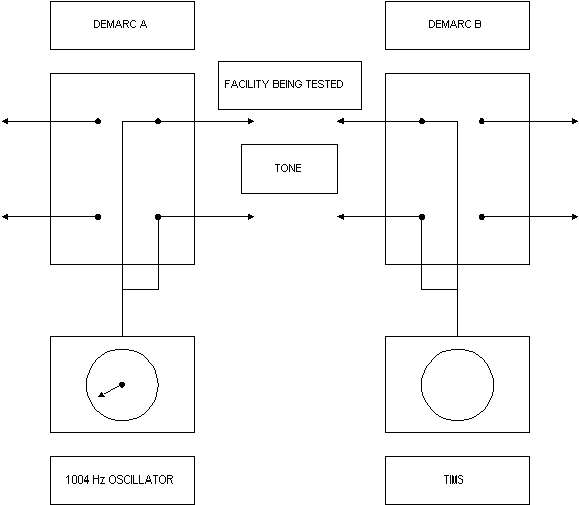
L’équipement est configuré pour tester le circuit entre le point de démarcation à A et le point de démarcation à B. Vous allez mesurer la perte de 1004 Hz inhérente au circuit entre A et B.
Les clips de pontage des deux cartes sont retirés afin d'isoler le segment du circuit soumis à l'essai.
À A, un oscillateur est attaché pour transmettre et recevoir des pistes (également appelées des pistes de pointe et de sonnerie). Au niveau B, un ensemble de mesure de transmission (TIMS) est attaché pour transmettre et recevoir des leads.
L'oscillateur à A est réglé pour générer une tonalité d'essai pure avec une puissance de 1 mW à 1004 Hz. Au point de démarcation B, le TIMS est configuré pour une puissance de lecture de l'ordre de 1 mW. La puissance de lecture à B est de 0,5 mW. Par conséquent, la puissance perdue entre A et B est :
1 mW – 0.5 mW = 0.5 mW
Une façon plus utile d'exprimer la perte est en termes de perte relative, ou le rapport entre la puissance de sortie (B) et la puissance de (A) :
Relative loss = Power out (B)
——————————————
Power in (A)
Relative loss = 0.5 x 10-3
——————————————
1 X 10-3
Relative loss = 0.5
Half the power that the 1004 Hz test-tone introduced at A is lost by the time
it reaches B.
Cet exemple montre comment répéter le test avec moins de puissance de la tonalité de test. L'oscillateur au point de démarcation A est réglé pour générer une tonalité de 1004 Hz à une puissance de 0,1 mW. Au point de démarcation B, la puissance mesurée est de 0,05 mW. Ensuite, la perte de puissance absolue est :
0.1 mW – 0.05 mW = 0.05 mW
La perte relative, ou le rapport entre la puissance de sortie (B) et la puissance de (A), est :
Relative Loss = Power out(B)
——————————————
Power in (A)
Relative Loss = 0.05 x 10-3
—————————————
1 x 10-3
Relative Loss = 0.5
La perte relative, ou rapport de puissance entre B et A, est la même que vous utilisiez un signal de test de 1 mW ou 0,1 mw.
Le décibel
Mathématiquement, le décibel est une mesure logarithmique. Le logarithme, ou log, d'un nombre donné est la puissance mathématique à laquelle un nombre de base doit être élevé pour obtenir le nombre donné. Le numéro de base que vous utilisez pour traiter le décibel est 10. Par exemple, quel est le logarithme (log) de 100 ? Une autre façon de poser cette question est de savoir à quel pouvoir obtenez-vous 10 pour obtenir 100 ? La réponse est 2 parce que 10 x 10 = 100.
De même,
log (100)= 2
log (1000)= 3
log (10,000)= 4
et ainsi de suite.
Vous pouvez également utiliser des logarithmes pour exprimer des quantités fractionnelles. Par exemple, quel est le logarithme de 0,001 ? Une autre façon de poser cette question est de savoir à quel pouvoir augmentez-vous 1/10 (0,1) pour obtenir 0,001 ? La réponse est 3. Par convention, le journal d'un nombre fractionné est exprimé comme négatif.
log (0.001) = -3
Les logarithmes de nombres qui ne sont pas des puissances intégrales de 10 peuvent être calculés lorsque vous les regardez dans une table ou lorsque vous utilisez une calculatrice manuelle.
Le décibel utilise des logarithmes pour exprimer les rapports de puissance. Par définition, le deciBel, ou dB, est le rapport logarithmique (base 10) de deux puissances, P1 et P2 donné par :
dB = 10 log P2
——
P1
P2 et P1 sont des mesures de puissance exprimées en unités cohérentes. Le nombre de décibels est positif si P2 est supérieur à P1. Le nombre est négatif si P1 est supérieur à P2 (voir le tableau). Il est important que les deux puissances soient exprimées dans les mêmes unités, telles que milliwatt (mW) ou watt (W). Sinon, cela entraîne des erreurs de calcul.
| Rapport de puissance | Valeur dB |
|---|---|
| 2 | 3 * |
| 4 | 6 * |
| 8 | 9 * |
| 10 | 10 |
| 100 | 20 |
| 1000 | 30 |
| 100000 | 50 |
| 1000000000 | 90 |
* Valeur approximative en dB.
Le rapport de puissance entre la puissance mesurée à B et la puissance mesurée à A était de la moitié. Exprimé en décibels :
(Loss, A to B) = 10 log (0.5) (Loss, A to B) = –3 dB
Avec l'utilisation de décibels, vous pouvez exprimer la perte ou le gain d'un circuit ou d'un équipement sans avoir à indiquer explicitement les valeurs réelles de la puissance d'entrée et de sortie. Dans l'exemple, la perte entre A et B est toujours de 3 dB, quelle que soit la quantité absolue de puissance transmise.
Mesure décimale par rapport à un milliwatt
La puissance absolue est exprimée en milliwatts et la puissance relative est exprimée en décibels. Lorsque vous établissez une relation entre le décibel et le milliwatt, vous pouvez éliminer le milliwatt en tant qu'unité de mesure opérationnelle et traiter exclusivement avec le décibel et les unités de mesure connexes. L'unité de mesure utilisée pour exprimer le pouvoir absolu en décibels est dBm.
dBm = 10 log (Power, measured in mW)
—————————————————————————
1 mW
Comme un milliwatt est la référence de puissance standard dans les communications, il est logique que 0 dBm (référence de puissance absolue lorsque des unités décibelles sont utilisées) soit égal à 1 mW de puissance. Mathématiquement :
0 dBm = 10 log Power out
——————————
Power in
0 dBm = 10 log (1/1)
0 dBm = 10 x 0 = 0
Étant donné que la puissance est une forme d'onde de courant alternatif et que l'impédance peut varier en fonction de la fréquence, il est nécessaire d'indiquer sur quelle fréquence la norme 0 dBm est basée. La fréquence standard est de 1004 Hz.
Vous devez également connaître la résistance ou l'impédance (charge) du circuit. L'impédance standard est de 600 ohms.
Par conséquent, la référence de 0 dBm est égale à 1 mW de puissance imposée à une impédance de 600 ohms d'une fréquence de 1004 Hz.
Les tests sont généralement effectués à l'aide de signaux de test moins puissants que 1 mW (0 dBm). Si vous appliquez une tonalité de test de 1004 Hz de -13 dBm à A, vous lisez -16 dBm sur le TIMS à B. La perte est toujours de -3 dB.
Point de niveau de transmission
Dans toute discussion sur les performances d’un circuit, il est nécessaire de décrire la puissance à un point particulier d’un circuit en référence à la puissance présente à d’autres points du circuit. Il peut s'agir de la puissance du signal, du bruit ou des tonalités de test.
La description de cette puissance est similaire à la description de la hauteur d'une montagne (ou de la profondeur de l'océan). Pour mesurer la hauteur d'une montagne, il est nécessaire de choisir une hauteur de référence à partir de laquelle mesurer. La hauteur de référence standard est le niveau de la mer, auquel est attribuée arbitrairement une hauteur de zéro. Quand on mesure toutes les montagnes du niveau de la mer, on peut comparer leur hauteur même si elles peuvent être éloignées de plusieurs kilomètres.
Cette figure montre la transmission de tonalité de test de la valeur A à la valeur B.

De la même manière, la puissance, aux points spécifiés dans un circuit, peut être décrite en termes de puissance à un point de référence standard.
Ce point, analogue au niveau de la mer, est appelé point de niveau de transmission zéro, ou TLP 0.
Tout autre TLP peut être référencé à la TLP 0 en additionnant algébriquement les gains et les pertes de 1004 Hz du TLP 0 au point de mesure.
La puissance présente à un point particulier d’un circuit dépend de la puissance à la source du signal, de l’endroit où la source est appliquée et de la perte ou du gain entre les deux points en question.
Avec l'utilisation du concept 0 TLP, la puissance d'un circuit est décrite en indiquant quelle puissance serait si elle était mesurée avec précision au TLP 0. La notation standard est dBm0, ce qui signifie que la puissance référencée au TLP 0.
Par exemple, le terme -13 dBm0 signifie que la puissance au TLP 0 est -13 dBm. Un TIMS correctement configuré mesure -13 dBm au niveau du TLP 0. Exemple de signal -13 dBm0.
Une fois que la puissance au TLP 0 est trouvée, la puissance à tout autre point du circuit peut être facilement déterminée. Par exemple, si le signal est de -13 dBm lorsqu'il est mesuré à la valeur TLP 0, il est inférieur de l3 dB à la valeur numérique de tout TLP sur le circuit lorsqu'il est mesuré à cette valeur TLP.
Si le signal est de -13 dBm au TLP 0 (ce qui en fait un signal de -13 dBm0), la puissance au TLP +5 peut être calculée comme le montre le résultat suivant :
(TLP) + (Power at the 0 TLP) = Power at the +5 TLP) (+5)+(–13 dBm0) = –8 dBm
Si le signal -13-dBm0 est correctement mesuré au TLP +5, le compteur affiche -8 dBm.
De la même manière, si un signal -13 dBm0 est mesuré à -3 TLP, le compteur affiche -16 dBm :
(TLP) + (Power at the 0 TLP) = (Power at the –3 TLP) (–3)+(–13 dBm0) = –16 dBm
Afin de déterminer la puissance attendue à un TLP donné, il suffit de connaître la puissance présente à un autre TLP dans le circuit. Et, comme la montagne n'a pas besoin d'être près de la mer pour déterminer sa hauteur, le TLP 0 n'a pas à exister sur le circuit.
Cette figure illustre un circuit entre deux démarques. Un signal de tonalité de test de -29 dBm est appliqué au TLP de -16. Que devez-vous mesurer au TLP +7 ?
Même si le TLP 0 n'existe pas sur le circuit, vous pouvez décrire la puissance que vous voyez au TLP 0 s'il existe :
TLP)+(Power at 0 TLP) = (Power at the –16 TLP)
(–16)+(Power at 0 TLP) = –29 dBm
(Power at 0 TLP) = –13 dBm
En utilisant à nouveau la relation, vous pouvez déterminer l'alimentation au TLP + 7 :
(TLP)+ (Power at 0 TLP) = (Power at + 7 TLP) (+7)+(–13 dBm0) = –6 dBm
L'utilisation de la référence 0 TLP permet d'indiquer les objectifs de transmission et les résultats mesurés indépendamment de tout TLP spécifique, et sans préciser les niveaux de tonalité d'essai ou l'endroit où la tonalité d'essai doit être appliquée.
Cette figure montre une transmission de tonalité de test de la valeur de demarc A à la valeur de demarc B.

Unités de mesure du bruit
Outre la description de la puissance de la tonalité d'essai à divers points d'un circuit, des unités de mesure reliées au décibel peuvent être utilisées pour décrire le bruit présent dans un circuit.
Brn
Pour décrire la puissance dans un circuit, le terme dBm est utilisé, c'est-à-dire la puissance référencée à 1 mW. Comme le bruit contient généralement beaucoup moins de 1 mW de puissance, il est pratique d'utiliser une puissance de référence beaucoup plus petite que 1 mW. La puissance de référence utilisée dans la description du bruit est de -90 dBm. La notation utilisée pour décrire le bruit en termes de bruit de référence est dBrn. Si vous connaissez le niveau de bruit en dBm, vous pouvez facilement mesurer le bruit dans dBrn :
dBrn = dBm + 90 dB
Par exemple, une mesure du bruit de 30 dBrn indique un niveau de puissance de -60 dBm (30 dB au-dessus du niveau de bruit de référence de -90 dBm). Ce tableau montre la relation entre dBm0 et dBrn.
| dBm0 | Valeur dB |
|---|---|
| 0 | 90 |
| -10 | 80 |
| -20 | 70 |
| -30 | 60 |
| -40 | 50 |
| -50 | 40 |
| -60 | 30 |
| -70 | 20 |
| -80 | 10 |
| -90 | 0 |
DBrnC
Le bruit contient de nombreuses formes d'onde irrégulières qui ont une large gamme de fréquences et de puissances. Bien que tout bruit superposé à une conversation ait un effet d'interférence, des expériences ont montré que l'effet d'interférence est le plus important dans le milieu de la bande de fréquences vocales.
Afin d'obtenir une mesure utile de l'effet d'interférence du bruit, les différentes fréquences qui contribuent au bruit global sont pondérées en fonction de leur effet d'interférence relatif. Cette pondération s'effectue par l'utilisation de réseaux de pondération, ou filtres, au sein du TIMS.
Les mesures du bruit à travers un réseau de pondération des messages C sont exprimées en unités de BrnC (bruit au-dessus du bruit de référence, pondération des messages C).
DBrnCO
Comme pour la puissance de la tonalité de test, la puissance acoustique peut être référencée au TLP 0.
Par exemple, si l’objectif de bruit du circuit est 31 dBrnC0, quelle est la mesure du bruit au niveau du TLP +7 ?
TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(+7) + (31 dBrnC0) = 38 dBrnC
La mesure du bruit au TLP +7 est de 38 dBrnC.
Quelle est la mesure du bruit au niveau du TLP -16 ?
(TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(–16) + (31 dBrnC0) = 15 dBrnC
La mesure du bruit à -16 TLP est de 15 dBrnC.
Informations connexes
Contacter Cisco
- Ouvrir un dossier d’assistance

- (Un contrat de service de Cisco est requis)
 Commentaires
Commentaires